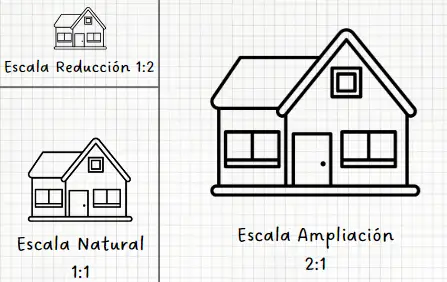
Las escalas se utilizan en dibujo técnico cuando se necesita dibujar un objeto que no cabe en el papel en el que se desea dibujar, utilizamos una escala de reducción. O quizás porque el objeto que deseamos dibujar es muy pequeño en la realidad y queremos mostrar más detalles en el dibujo, utilizamos una escala de ampliación. Pero antes de esto debes saber qué son las escalas, qué tipos de escalas existen y para qué sirve cada escala.
¿Qué son las escalas?
La escala es la relación que existe entre el tamaño de un dibujo y el tamaño del objeto real.
La escala empleada en los dibujos suele indicarse mediante una proporción.
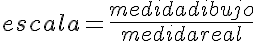
Las escalas son factores de multiplicación de las medidas del objeto, para poder hacer las representaciones de su dimensiones en los papeles de los que disponemos.
Tipos de escalas
Escala natural o real
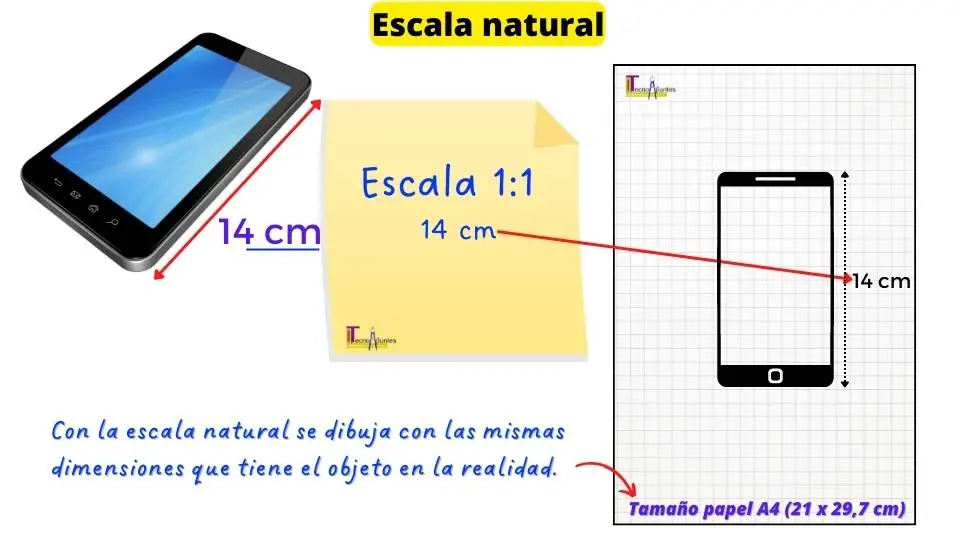
Es la manera más fácil de dibujar un objeto ya que con la escala natural se dibuja con las mismas dimensiones que tiene el objeto en la realidad.
Así podemos hacernos una idea rápida de qué tamaño tiene el objeto en la realidad con tan solo mirar su dibujo. La escala natural también se denomina escala 1:1 (se lee «escala uno uno»).
Escala de reducción
Lo más habitual es que el objeto que queremos representar sea grande y su dibujo a escala 1:1 no quepa en el papel. Entonces deberemos dibujarlo reduciendo proporcionalmente su tamaño, utilizaremos una escala de reducción.
Que la escala sea 1:2 significa que una unidad de medida en el papel representa dos unidades en el objeto real. Se lee «escala uno es a dos». Las escalas se determinan en función de las necesidades. Pueden ser 1:5, 1:10, 1:25, etc.
Cómo dibujar un objeto con la escala de reducción
Para dibujar un objeto con escala de reducción se deben dibujar todas sus medidas dividiéndolas antes por un número que siempre debe ser el mismo.
Observa el ejemplo de la imagen de la torre Eiffel que tiene una altura de 320 metros.
Queremos hacer un dibujo que quepa en un papel de tamaño A0 (84,1 x 118,9 cm) por lo que dividiremos la altura de la torre Eiffel por 300.
En este caso estamos utilizado una escala 1:300 (se lee «escala uno a trescientos»).
Esto quiere decir que 1 unidad de longitud en el dibujo (1 cm, por ejemplo) equivale a 300 unidades de longitud en el objeto real (300 cm o 3 m de la torre Eiffel en la realidad).
Fíjate como la altura de 320 metros de la torre Eiffel dibujada a una escala de reducción 1:300 mide en el papel 1,06 metros.
Escalas de reducción normalizadas
En general se puede utilizar cualquier número entero como escala, por ejemplo 1:6, 1:13, 1:27, pero se recomienda utilizar las escalas normalizadas como las que vienen dadas en las siguiente imagen.
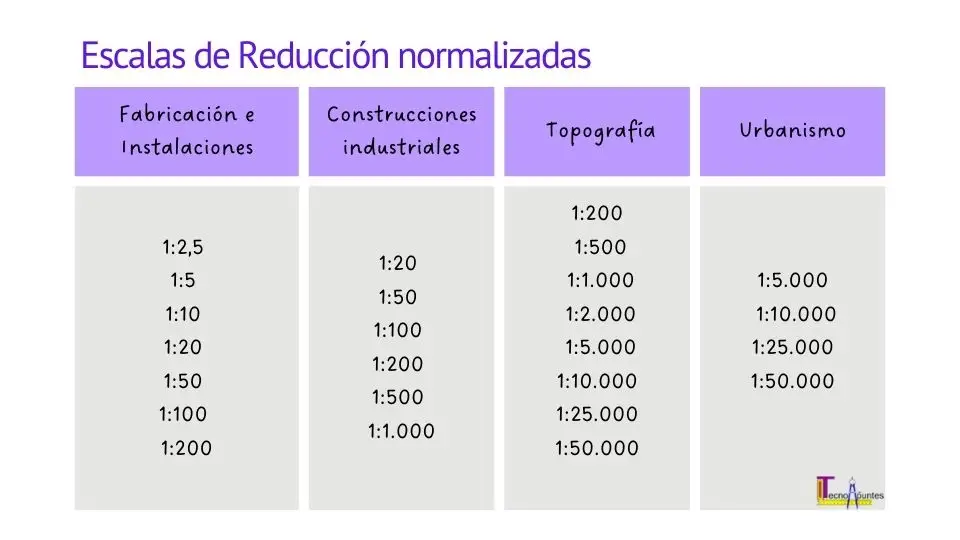
El número de la derecha indica la reducción aplicada. Por ejemplo, la escala 1:100 («uno a cien»), indica que el dibujo se ha reducido 100 veces respecto del objeto real.
Observa como en nuestro ejemplo de la torre Eiffel la escala 1:300 no está normalizada.
Para construcciones industriales se puede elegir la escala 1:200 o la 1:500.
Descartamos la escala 1:200 ya que 320 m / 200= 1,6 m y deberíamos realizar un dibujo de 1,6 m de alto, siendo mayor que las medidas del papel.
Para seleccionar una de las escalas normalizadas se ha de tener en cuenta el tamaño del papel y ver cómo quedaría el dibujo en la escala elegida.
Elegimos la escala 1:500, por lo que la altura de la torre Eiffel en el dibujo será de 320 m / 500 = 0,64 m o lo que es lo mismo 64 cm de altura en el dibujo.
Como hay que dejar un espacio alrededor del dibujo, cuando vayas a realizar el dibujo, ten en cuenta que no debe ser ni demasiado grande, ni demasiado pequeño.
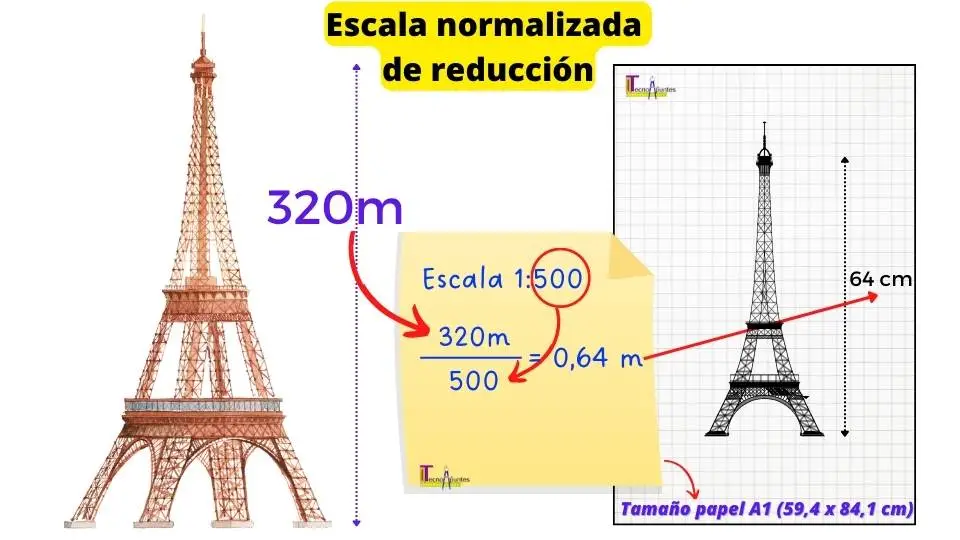
Como puedes observar en la imagen, al elegir una escala 1:500 podemos realizar el dibujo en un papel con el tamaño A1, ya que tiene una altura de 84,1 cm por lo que nos cabría nuestro dibujo de la torre Eiffel.
E incluso nos sobrarían 10,05 cm tanto por la parte superior como por la inferior del dibujo. (64 + 10,05 + 10,05 = 84,1 cm)
Escala de ampliación
La escala de ampliación se utiliza para representar objetos que son muy pequeños en la realidad y se quieren dibujar con el máximo detalle.
Normalmente se emplea la escala de ampliación para dibujar objetos, como componentes electrónicos, tornillos, engranajes de reloj, etc. El dibujo de estos objetos a escala natural (1:1) quedaría demasiado pequeño.
Las escalas de ampliación se determinan en función de las necesidades. Se recomienda utilizar las escalas de ampliación normalizadas que son 2:1, 5:1, 10:1, 20:1, 50:1, 100:1
Que la escala sea 2:1 «escala dos a uno», significa que dos unidades de medida en el papel representan una unidad en el objeto real. El tamaño en el dibujo es el doble que el tamaño del objeto en la realidad.
Cómo dibujar un objeto con la escala de ampliación
Vamos a ver un ejemplo práctico de escala de ampliación con el sacapuntas de la figura que medimos con el calibre o pie de rey.
Te puede interesar: Cómo realizar medidas con el calibre o pie de rey.
Como puedes observar en la figura, la regla del pie de rey muestra que el sacapuntas mide 14,6 milímetros en la realidad.
Si deseamos realizar un dibujo del sacapuntas con escala de ampliación normalizada en un papel del tamaño A4 (21×29,7 cm) debemos elegir la escala de ampliación normalizada 10:1 para que quepa en el papel.
Solo hay que dibujar todas sus medidas multiplicándolas por el número de la escala que hemos elegido. En nuestro caso multiplicaremos x 10. Esto quiere decir que 10 unidades en el dibujo equivalen a 1 unidad de longitud del sacapuntas en la realidad.
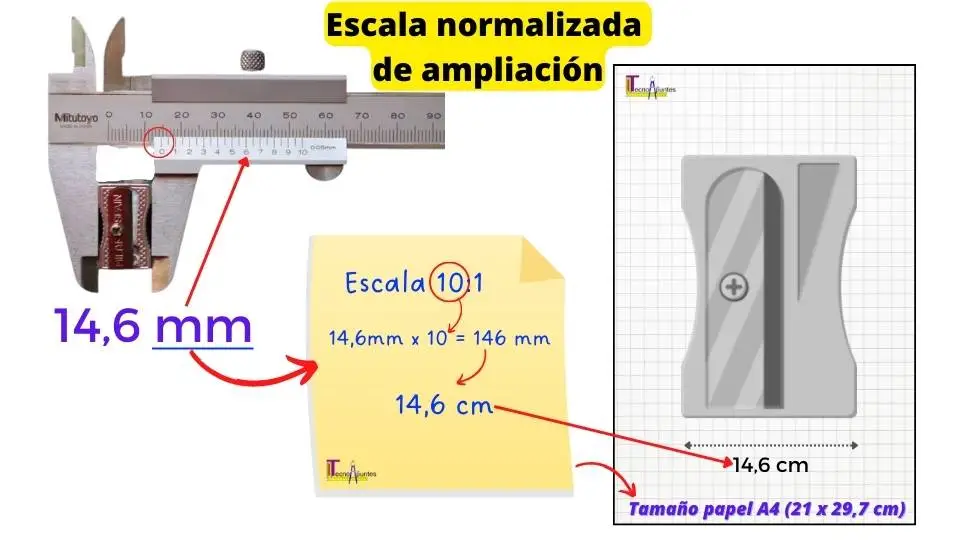
Como puedes observar en la figura, al multiplicar por 10 ampliamos 10 veces la medida real. Por lo que los 14,6 mm equivalen a 146 mm en el dibujo (14,6 cm).
Si elegimos el tamaño de papel A4, podemos dibujar el sacapuntas en el centro del dibujo y tendremos a cada lado del dibujo un espacio libre de 3,2 cm. (14,6 + 3,2 +3,2 = 21 cm)
Tutorial – Escalas: conceptos de escalas
Y si todavía no tienes claro qué son las escalas y cómo se calculan las escalas, te dejo aquí un vídeo explicativo de los conceptos más básicos de escalas. Échale un ojo porque te va a venir muy bien para luego contestar las preguntas del test de escalas.
Test de escalas
Si ya sabes lo que son las escalas, los tipos y tienes a mano una hoja para hacer cálculos, puedes practicar con este test sobre escalas de dibujo técnico donde te propongo que respondas a los siguientes ejercicios de escalas.
Sobre una carta marina a escala 1:50.000, se mide una distancia de 8,5 cm entre dos islotes ¿Qué distancia real hay entre ambos?
¿Qué escala se está empleando si la longitud de una barra metálica es de 1000 cm y en su representación gráfica su longitud es de 25 cm?
Si en un plano de ciudad, dos localidades están separadas por 25 cm. ¿Cuál es su distancia si real si la escala del plano es de 1:50.000?
¿Qué escala se está empleando si la longitud de una barra metálica es de 10 m y en su representación gráfica su longitud es de 5 cm?
Si en un plano dos pueblos se encuentran separados por 5cm, y en la realidad los separan 2 km. ¿Cuál es la escala del plano?
¿A que medida real en Km correspondería 22 mm de un mapa, si este está realizado a una escala 1:500.000?
En una escala 1:100 donde las medidas del dibujo son 30 mm. ¿Qué medidas en cm tendrá el objeto en la realidad?
El dibujo de la cabeza de un tornillo, dibujado a escala 10:1 mide 125 mm. ¿Cuánto mide realmente la cabeza del tornillo en cm?
Con una escala de 1:30. ¿Qué medida tendrá en el plano una pared de 6 metros de longitud?
¿Qué escala se está empleando si la longitud de una carretera es de 50 km y en su representación gráfica en un plano es de 20 cm?
Share your Results:
Ejercicios prácticos de escalas
Si deseas descargar una hoja de ejercicios prácticos de escalas para practicar en clase lo aprendido aquí sobre escalas, puedes descargarla en PDF e imprimirla gratis.
Consta de 5 problemas variados en los que el alumno debe dibujar una casa en distintas escalas.
También se propone que realice diversos cálculos, e incluso mediciones sobre el papel para averiguar las escalas utilizadas.
Para asegurar que no eres un robot o spam malicioso intentado descargar el archivo de «Práctica con problemas de escalas«, rellena el siguiente formulario y recibirás un enlace con el archivo en PDF listo para imprimir.
Práctica – Ejercicios de Escalas
Dibujos a Escala – Fichas de ejercicios prácticos
Puedes imprimir unas fichas con ejercicios prácticos para dibujar a escala en papel cuadriculado. Deberás realizar los dibujos a escala de ampliación y de reducción desde el dibujo en escala natural.
Preguntas frecuentes y consejos
Quizás estos artículos de tecnologías que también te pueden interesar. 👇
